Practice: Machine Learning Questions

Question 0

Consider the dataset shown in the following table. Assume this is stored in a DataFrame named df .

ColA	ColB	ColC
a	1	a
c	2	z
b	3	a

How many columns will the result of pd.get_dummies(df) have? Enter result as an integer (e.g. 4 ).

Your Task

Write your answer down in your own space.

Question 1

Consider the dataset shown in the following table. Assume this is stored in a DataFrame named df .

ColA	ColB	ColC
a	1	a
c	2	z
b	3	a

How many rows will the result of pd.get_dummies(df) have? Enter result as an integer (e.g. 4 ).

Your Task

Write your answer down in your own space.

Question 2

Consider the general task of assessing performance of a machine learning model. Which of the following options best describes why we needed to introduce a test set to evaluate the future performance of the model?

Your Task

Select one option. Write your answer down in your own space.

Option 0

The training set has more data than the test set.

Option 1

The test set has more data than the training set.

Option 2

The test set hasn’t been seen by the model when training.

Option 3

The test set is higher quality than the training set.

Question 3

Consider a particular model for a regression task called polynomial regression. Polynomial regression tries to fit the “curve” of best fit to the data to minimize the mean squared error.

In its simplest form, it is just linear regression, where we learn an equation \(y = mx + b\) where \(m\) and \(b\) are inferred from the data. This is shown on the left in the picture below. We could also do quadratic regression that fits a curve \(y = ax^2 + bx + c\) where \(a\), \(b\), and \(c\) are inferred from the data. This is shown in the middle in the picture below. In its general form polynomial regression uses some hyperparameter \(p\) to fit a polynomial of degree \(p\) to the data. Linear regression is just a special case where \(p=1\) and quadratic regression is a special case when \(p=2\). A polynomial of high degree \(p\) is shown in the plot on the right.

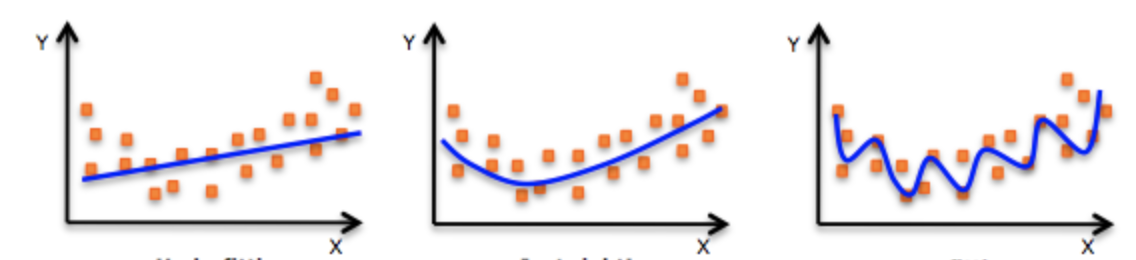
This question asks about the model complexity as we change this hyperparameter \(p\).

As we increase \(p\) what happens to the complexity of the model?

Your Task

Select one option. Write your answer down in your own space.

Option 0

It increases

Option 1

It doesn’t change

Option 2

It stays the same

Question 4

This question uses the same set up of polynomial regression from the last question:

Select the option below that best describes the answer.

If we use a polynomial with very high degree \(p\), would we expect that the training error is higher or lower than a model with low degree \(p\) (e.g., linear regression)? In other words as \(p\) increases in degree, would we expect the training error to go up or down?

Notice we are talking about error and not accuracy. Remember error is a measurement of how “wrong” the model is.

Your Task

Select one option. Write your answer down in your own space.

Option 0

The training error should go up as \(p\) increases

Option 1

The training error should go down as \(p\) increases